
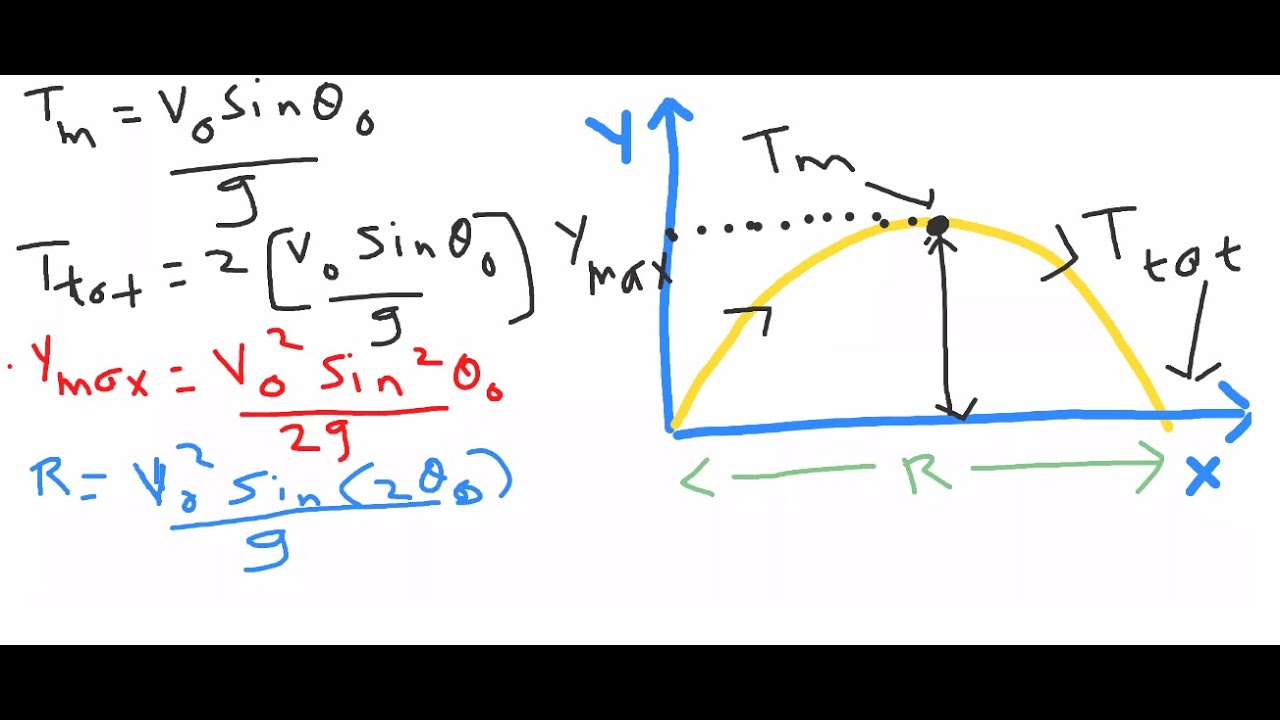

For a given velocity of projection the range will be maximum when sin 2 1, 2 90° & 45° For entire motion, y 0 and x R 0 tan R g 2 vi 2 cos2 R2 g 2. y H + x tan x 2 g 2 u 2 ( 1 + tan 2 ), and its maximum range is. Equation for horizontal range The equation of trajectory of projectile is given by, y tan x g 2 vi 2 cos2 x2 This is the equation for horizontal range.

The ProblemĪ cannon sits on top of a plane at a height #h# above the ground and fires a shell with an initial velocity #v_0#. Launch angles closer to 45 45degree 4545, degree give longer maximum horizontal distance (range) if initial speed is the same (see figure 5 above). If a projectile is launched at a speed u from a height H above the horizontal axis, g is the acceleration due to gravity, and air resistance is ignored, its trajectory is. A number of interesting methods of solution arose so the idea of this article is to present all of these since each method illustrates a different approach to the problem and each is instructive in its own right. A recent homework problem that appeared in the forums was concerned with maximizing the horizontal range of a projectile subject to the launch site being a fixed height above the ground upon which the projectile eventually impacted.


 0 kommentar(er)
0 kommentar(er)
